排序算法学习总结

发表于 更新于 分类于 评论数： 阅读次数： 本文字数： 1.1k 阅读时长 ≈ 4 分钟

逃避是没有用的，困难不会因为你的逃避就迎刃而解。只有改变，才能迎来新的机遇。改变不了过去，就改变未来。改变不了别人，就改变自己。—-人民日报《[夜读] 生气不如争气，抱怨不如改变》

最近参加多场笔试及面试，察觉到自己的算法实现能力很弱，随决定翻看算法方面的书籍来加强这方面的学习及编码实现。因此，本文尽量总结所学，以备所需。温故而知新，坚持记录！

bubble-sort [冒泡排序]

基本思想

反复地交换顺序颠倒的相邻元素，第一轮迭代会将最小或最大元素交换到序列末端，以此类推，至多经过n-1轮迭代后会将含有n个元素的待排序列按升序或降序排好序。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/*
 * @array: specify a pending array
 * @len: the size of the @array
 */
void bubble_sort(int *array, int len)
{
    int i, j;

    for (i = 0; i < len - 1; i++) {
        int flag = 0;

        for (j = len - 1; j > i; j--) {
            if (array[j] < array[j - 1]) {
                flag = 1;
                array[j] ^= array[j - 1];
                array[j - 1] ^= array[j];
                array[j] ^= array[j - 1];
            }
        }
        if (!flag)
            return;
    }
}

考虑到一组序列可能不需要n-1轮迭代就能排好序，使用标志变量来优化掉不必要的元素比较，只要在下一轮迭代中没有发生相邻元素交换，其意味该序列已经排好序，再后来的迭代就是没必要的。

图例

bubble_sort

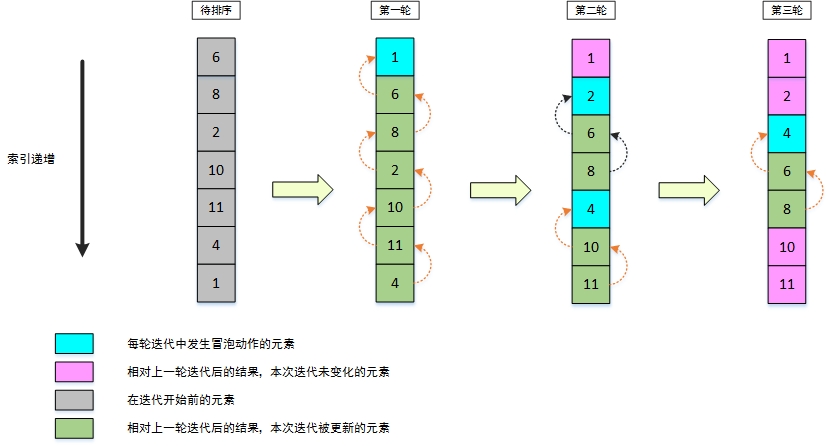
图1 冒泡排序图解
**带箭头虚线表示向上移动元素的轨迹，比如沿着箭头的反方向，在第一轮中就可以确定元素1是从低端一直移动到顶端；在第二轮中有两个元素向上移动。**

insert-sort [插入排序]

基本思想

每一轮迭代都将一个待排序元素插入到前面的有序序列中，直到把所有元素都插入到有序序列为止。这一过程分两步：

  • 在有序序列中寻找待排序元素的位置，将该位置后的所有有序元素向后移动为这个待排序元素腾挪空间
  • 将这个待排序元素放入这个空间

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void insertion_sort(int *array, int length)
{
    int i, j, key;

    for (j = 1; j < length; j++)
    {
        key = array[j];
        i = j - 1;

        /*
         * array[i] > key statement, ascending sorting.
         * array[i] < key statement, descending sorting.
         *
         */
        while (i >= 0 && array[i] > key)
        {
            array[i + 1] = array[i];
            i--;
        }
        array[i + 1] = key;
    }
}

上面代码是先读取所有待排序元素，然后排序这个序列。其实也可以一边读取待排序元素一边排序，最终使这个序列排好序。

图例

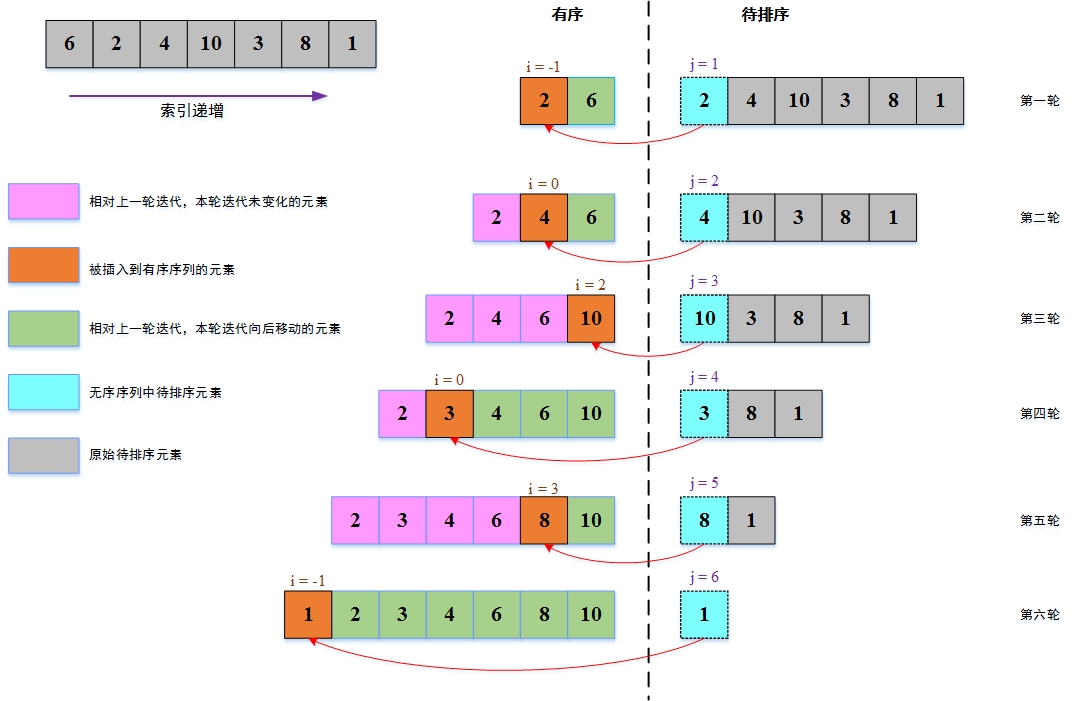
insert_sort

图2 插入排序图解
**注意：i， j表示数组的索引位置，比如j=1意味着原数组的第二个元素将被插入有序序列中， i=-1意味着有序序列的第一个位置用来存放待排序元素** ### select-sort [选择排序] #### 基本思想 每一轮迭代从待排序序列中找出最小元素，然后与待排序序列的第一个元素交换，直到执行n-1轮迭代使所以元素排好序。因为到第n-1轮时，就剩余两个待排序元素了，本轮迭代不管有没有发生交换都会将输入序列排好序。 #### 示例代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void select_sort(int *array, int len)
{
    int least, i, j;
    for (i = 0; i < len - 1; i++)
    {
        least = i;
        for (j = i; j < len; j++)
        {
            if (array[j] < array[least]) {
                least = j;
            }
        }
        if (least != i) {
            array[i] ^= array[least];
            array[least] ^= array[i];
            array[i] ^= array[least];
        }
    }
}
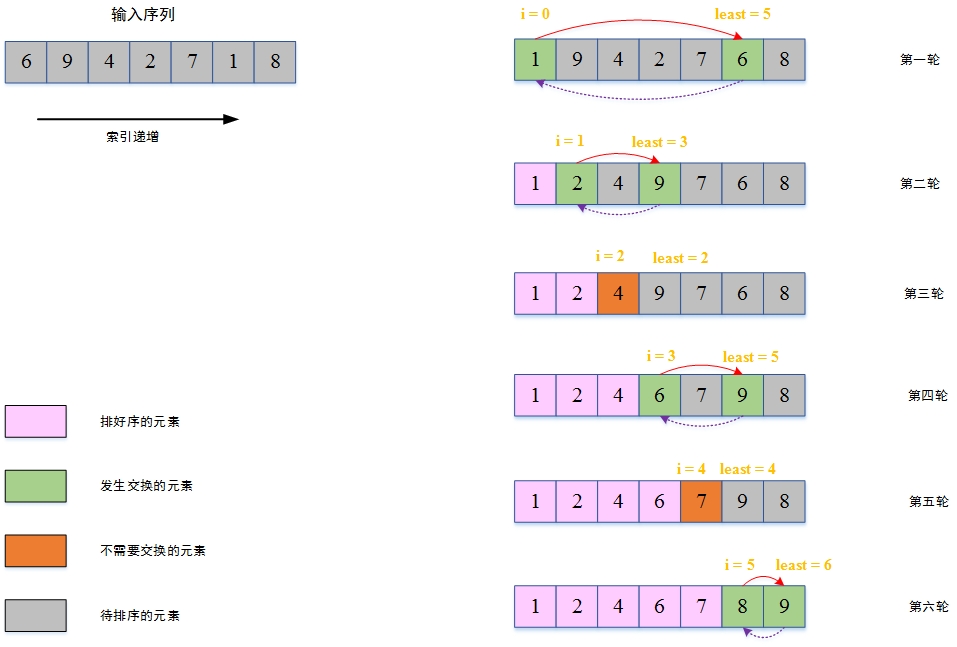
#### 图例 ![select_sort](/images/19/select-sort.jpg)
图3 选择排序图解
**注意： 图中粉红色元素属于有序序列，其后面就是待排序序列** ### 小结 ### merge-sort [合并排序] 基本思想： ### quicksort [快速排序] ### heapsort [堆排序]

性能对比与分析总结

Tips

两变量交换

1. 三变量法

1
2
3
tmp = a;
a = b;
b = tmp

此方法适用范围广，推荐使用

2. 变量加减法

1
2
3
a = a + b
b = a - b
a = a - b

这个方法看起来很好，少用一个中间变量，但是实际上很少使用，因为其适用范围很窄：只有定义了加减运算的数据类型才能使用这种方法。
3. 变量异或运算法

1
2
3
a ^= b
b ^= a
a ^= b
1
a ^= b ^= a ^= b

不建议使用这个方法，一般只能适用整数类型的变量。